关于二叉树的种类:
一、满二叉树
满二叉树:
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。深度为k,有2^k-1个节点的二叉树。
二、完全二叉树
完全二叉树:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^h -1 个节点。
我们可以给完全二叉树编号,这样父子之间就可以通过编号轻松求出。
比如我给所有节点从左到右从上到下依次从 1 开始编号。
那么已知一个节点的编号是 i,那么其左子节点就是 2 i,右子节点就是 2 1 + 1,父节点就是 (i + 1) / 2。
二叉树的最大宽度
一、序列化二叉树
二叉搜索树
二叉搜索树是有数值的了,二叉搜索树是一个有序树。
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树
二、平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
对于一个二叉查找树,常规操作有插入,查找,删除,找父节点,求最大值,求最小值。
核心:二叉搜索树的中序遍历的结果是一个有序数组
例题:
验证二叉搜索树
二叉搜索树迭代器
二叉树的遍历
一个中心
三、树的遍历:
遍历不是目的,遍历是为了更好地做处理,这里的处理包括搜索,修改树等。
树虽然只能从根开始访问,但是可以选择在访问完毕回来的时候做处理,
还是在访问回来之前做处理,这两种不同的方式就是后序遍历和先序遍历。
其中有两个重要知识点:
DFS(深度优先遍历)
BFS(宽度优先遍历)
二叉树的遍历结构:就是找根节点
前序:根-左-右
中序:左-根-右
后序:左-右-根
举个例子:
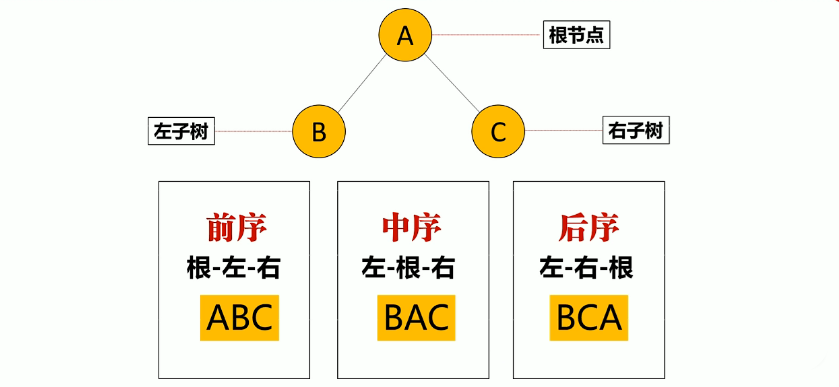
前序就是根节点在前
中序就是根节点在中
后序就是根在后
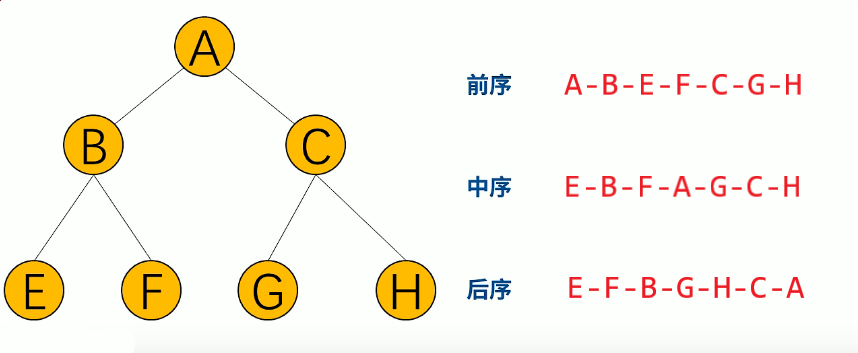
ps:
以上就是对二叉树的详细介绍了,
如果这篇文章对您有帮助,可以在下方进行留言
下面的赏是对我最大的鼓励。
您的鼓励就是我最大的动力!
资料参考于课本,csdn开发者论坛,博客园开发者论坛…
转载请注明出处https://lil-sum.github.io/, 感谢配合.


